Fondamenti di Elettronica:
test, seconda parte
Difficoltà: *
L'amplificatore di figura presenta una resistenza di ingresso pari a 10 kohm. Sapendo che l'amplificatore operazionale utilizzato si può considerare ideale, determinare la corrente i
O (in mA), erogata dall'amplificatore stesso, quando V
I è pari a 2 V.
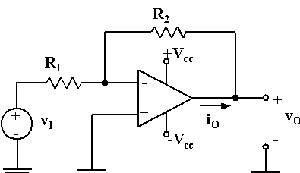
Utilizzare il punto come separatore ed inserire il valore numerico con due cifre decimali.
i
O (in mA) = -0.20
La resistenza di ingresso e' = R1, quindi la corrente che passa per R1 = 2/10k= 0.2 mA questa passa anche per R2 e torna con verso contrario a Io
Difficoltà: *
Dato lo specchio di corrente in figura, supponendo i transistori operanti in zona attiva diretta, determinare la corrente di uscita I
0 (trascurare l'effetto Early).
Dati: R = 1kOhm, V
EE= 4.7 V, V
BE= 0.7 V, b=18,
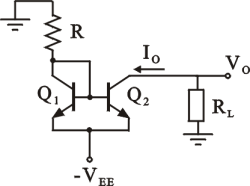 I0 = 3.6 mA
I0 = 3.6 mA
I
0 = 4.9 mA
I
0 = 0.6 mA
I
0 = 4.0 mA
La formula per gli esercizi sulle correnti a specchio DA IMPARARE e':
Io = Ic / (1+2/b)
Ic è la corrente che passa su R. Abbiamo che il collettore di Q1 a cui e' attacata R
e' alla tensione -Vee - Vbe che abbiamo e quindi alla tensione di -4V
La corrente Ic sara' dunque (-Vee -Vbe)/R, da cui Io = 3.6 mA
Difficoltà: *
Dato lo specchio di corrente in figura, supponendo i transistori operanti in zona attiva diretta, determinare la corrente di uscita I
0 (trascurare l'effetto Early).
Dati: R = 1kOhm, V
CC= 8.7 V, V
BE= - 0.7 V, b=18,
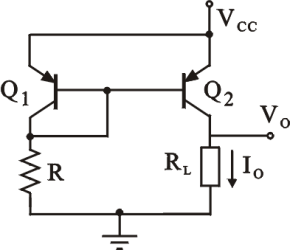
I
0 = 8.5 mA
I0 = 7.2 mA
I
0 = 0.6 mA
I
0 = 8.7 mA
La formula è : Io = Ic / (1+2/b)
Ic qui e' (in Q1) = (Vcc - Vbe) / R in quanto la base si trova a Vcc-Vbe=8V e la corrente di collettore e' quella che passa per R verso massa.
Allora IO = 7.2 mA
Difficoltà: *
L'amplificatore di figura è realizzato con un amplificatore operazionale che si può considerare ideale. Sapendo che la resistenza R
1 è pari a 120 kOhm e che il guadagno di tensione è pari a 1, determinare la potenza (in mW) erogata dall'amplificatore quando v
I è pari a 12 V.
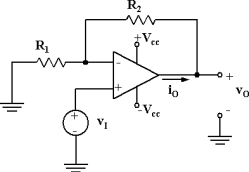
Utilizzare il punto come separatore ed inserire il valore numerico con due cifre decimali.
P
O (in mW) = 1.2
Su R1 passa la corrente Vi/R1. Questa e' la stessa che passa su R2, per l'idealita' dell'operazionale. La potenza sarà quindi P=V*I dove I1= I2 = Vi / R1
V1 = Vi, V2 = Vi(R2/R1 +1) - Vi = Vi * R2/R1
Ma, essendo il guadagno 1 ai capi di R2 c'è lo stesso potenziale e non passa corrente
Quindi Po= Vi^2 / R1.
Difficoltà: *
Dato il circuito di figura, determinare il valore della resistenza R
C (in kOhm) necessario affinchè il BJT presenti una tensione v
CE a riposo pari a 15 V (si trascuri l'effetto Early).
Dati: R
B=100kOhm, V
CC=25V, V
BE=0.7V, V
CEsat=0.8V, b
F=150
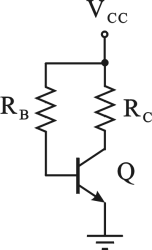
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con due cifre decimali
R
C (in kOhm) = 0.27
Essendo Vce = 15 V > VceSAT sono in zona attiva quindi
Vcc = ib * b0 * RC + Vce
Vcc = ib * Rb + Vbe
da cui ricavo ib = 0.243 mA, ic = 36.45 mA
e Rc = (Vcc - Vce)/ic = 274.35 ohm
Difficoltà: *
Dato il circuito di figura, determinare l'intervallo di valori della tensione di alimentazioneV
DD per il quale il MOSFET funziona in zona di saturazione.
Dati: R
G=50kohm, R
D=200ohm, V
T=4.8V, I
DSS=V
T2mC
oxW/2L=6mA
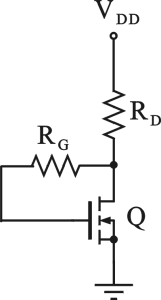
4.2V < V
DD < 7.4V
V
DD > 2.8V
V
DD < 9.8V
VDD > 4.8V
Per Rg non passa corrente, quindi Vgs=Vds
Le condizioni sono Vgs >Vt
e Vds>Vgs-Vt, questa, essendo Vt>0 e' sempre verificata
e' quindi sufficiente sia Vgs=Vds > Vt
Per esclusione scelgo Vdd>4.8
Difficoltà: *
Dato il circuito di figura, determinare il valore della resistenza R
D (in kOhm) richiesto per avere una tensione V
DS a riposo pari a 12 V.
Dati: R
G=100kOhm, V
DD=15V, V
T=7V, I
DSS=VT2mCoxW/2L=8mA
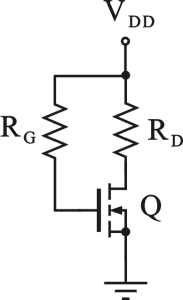
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con due cifre decimali
R
D (in kOhm) = 0.29
Abbiamo Vgs = VDD = 15 V
siamo quindi (dalla tabella) in saturazione, troviamo la corrente di drain
Id = IDSS ( 1 - VGS / VT )2 =10.45 mA
visto che VDD = Id * RD + VDS
RD = (VDD - VDS) / ID= 0.287 kOhm
Difficoltà: *
Dato il circuito di figura, supponendo il transistor operante in zona attiva diretta, determinare la potenza erogata dal generatore di corrente I
B.
Dati: R
C=5kW, V
BE=0.7 V, V
CC=10V, I
B= 10 mA, b=100
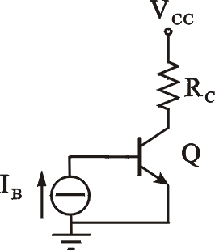
P
IB = 100 mW
PIB = 7mW
P
IB = 1 mW
P
IB = 70 mW
E' molto semplice. Il generatore eroga 10mA e ai suoi capi ci sono Vbe=0.7V
La potenza erogata sarà allora P=I*V = 7 mW
Difficoltà: *
La corrente di saturazione inversa di un diodo ideale (IS):
(NO) aumenta all'aumentare della polarizzazione inversa
aumenta all'aumentare della temperatura
(NO) aumenta all'aumentare del drogaggio
aumenta al diminuire dell'area di giunzione
[La formula è
Is = Aqni2( Dp /LpNd + Dn /LnNa )]
dove il termine ni dipende direttamente dalla temperatura...
Difficoltà: *
Calcolare la tensione che deve essere applicata ai capi di un diodo a giunzione PN per produrre, a temperatura ambiente, una corrente inversa pari al 95% della sua corrente di saturazione IS.
Dati:
Fattore di idealità: h=1
Potenziale termico: VT=25mV
Inserire il valore utilizzando il punto come separatore dei decimali ed utilizzando una cifra decimale.
Vd (in mV) = -74.9
deve essere
I = - 95/100 * IS
La formula e'
I = IS ( e ^ (VA/VT) - 1 )
quindi
e ^ (VA/VT) - 1 = - 0.95
VA = ( ln 0.05 ) * VT = - 74.9 mV
Difficoltà: *
Dato il circuito di figura, che utilizza un amplificatore operazionale ideale, determinare l'espressione dell'impedenza d'ingresso a frequenza infinita Z
IN(¥) vista dal generatore V
IN.
DATI: R
1=R, R
2=3R, R
3=2R, R
4=R, R
5=R
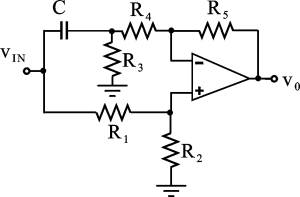
(NO) b) Z
IN(¥) = 2R
c) Z
IN(¥) = R
(NO) a) Z
IN(¥) = 2R/3
Cominciamo dicendo che Rin= Vi / Ii
dove Ii è la corrente che esce dal generatore di ingresso.
Ii è la somma di 3 contributi: il ramo che va verso il non invertente, il ramo di R3 e il ramo di R4.
=I+ + I3 + I4
I+=Vi / (R1+R2)
I3=Vi/R3
inoltre so che
V+ = Vi * R2 / (R1+R2) = V-
Quindi ai capi di R4 cade Vi-V+= Vi / 4
I4= Vi/4R4
Ottengo allora Ii = Vin / R
da questa ottengo Rin = R
Difficoltà: *
Il circuito di figura utilizza un amplificatore operazionale ideale. Determinare la Resistenza di ingresso Rin.
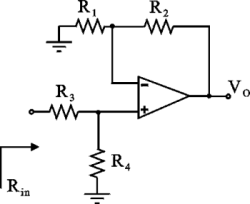
Rin = R
3
Rin = R3+R4
Rin = R
3+R
1
Rin = R
3 // R
4Ovvero, che resistenza c'è tra Vin e massa? C'è proprio la serie tra R3 e R4
Difficoltà: *
Sia data una barretta di semiconduttore drogata n in cui la densità di portatori di carica sia linearmente decrescente nella direzione x, come mostrato in figura. Si determini il valore della corrente di diffusione degli elettroni sapendo che le dimensioni della barretta di semiconduttore nella direzione perpendicolare ad x sono 10mm x 10mm.
Dati:
Concentrazione all'origine: n(0) = 1·10
15 [cm
-3]
Concentrazione all'estremità della barretta: n(x
1) = 1·10
12 [cm
-3]
Lunghezza della barretta di semiconduttore: x
1 = 1 [mm]
Carica dell'elettrone: q = 1.6·10
-19 [C]
Coefficiente di diffusione: D
n = 35 [cm
2/s]
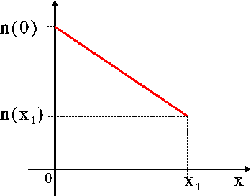
Inserire il valore utilizzando il punto come separatore dei decimali ed utilizzando una cifra decimale
|I
diff| (in mA) = -0.6
La formula per la densità di corrente in presenza di un gradiente di drogaggio e':
Jdiff = q * Dn * dn(x)/dx
Dove Dn è il coefficiente di diffusione, q la carica dell'elettrone e dn/dx la variazione di drogaggio
Da J la corrente si trova moltiplicando per l'area della sezione della barretta, quindi:
Idiff = q*Dn * (n1-n0)/x1 * A = (tengo tutto in cm, la lunghezza viene 0.1 cm... poi moltiplico per 10 per passare ai milliampere) = -0.55944 mA
Difficoltà: *
Sia data una barretta di semiconduttore drogato n con concentrazione di atomi donatori ND=4·1015 [cm-3]. Si determini il rapporto tra la densità di corrente di deriva di elettroni e quella di lacune derivanti dall'applicazione di una tensione VA alle estremità della barretta di semiconduttore.
Dati:
Concentrazione intrinseca: ni = 1.45·1010 [cm-3]
Carica dell'elettrone: q = 1.6·10-19 [C]
Mobilità degli elettroni: mn = 1260 [cm2/(V s)]
Mobilità delle lacune: mp = 460 [cm2/(V s)]
Inserire il valore normalizzato a 1010 ed utilizzando una cifra decimale.
Si ricordi di utilizzare il punto come separatore dei decimali.
Jndrift/Jpdrift = 20.8
Ci sono qui alcune formule da ricordare:
Conducibilità = sigma = q * numero di portatori * mobilità
Campo elettrico = E = V / lunghezza
Jdrift = sigma * E
quindi
Jndrift = q * Nd * mn * V / lunghezza
Jpdrift = q * ni * mp * V / lunghezza
Abbiamo Nd elettroni e Ni2/Nd lacune (portatori minoritari)
Jn / Jp = (Nd * mn) / ( (ni2/ Nd) * mp) = 20.84 E 10
Difficoltà: *
Sia data una barretta di semiconduttore drogata n alle estremità della quale viene applicata una differenza di potenziale pari a V
A = 0.5 V. Si determini la velocità media di deriva dei portatori maggioritari sapendo che la loro mobilità varia in funzione della concentrazione di droganti in accordo con il grafico di figura.
Dati:
Concentrazioni di droganti: N
D = 3 E 16 [cm
-3]
Lunghezza della barretta di semiconduttore: L = 100 [μm]
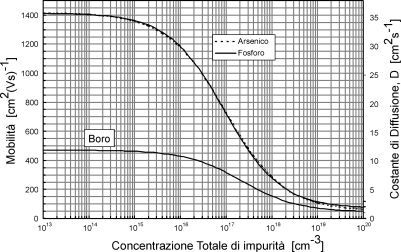
Inserire il valore utilizzando il punto come separatore dei decimali ed utilizzando una cifra decimale
|vdrift| (in m/s) = 500
Altra formula da ricordare:
La velocità di deriva = μ * E
dal grafico trovo che μ = 1000 per ND = 3*E 16
vsdrift = μ * VA / lunghezza = (tengo tutto in cm, la lunghezza è 0,01cm e poi divido per 100)
Difficoltà: *
Il circuito di figura, rappresenta un transistore MOSFET a canale n polarizzato in zona di saturazione con relative caratteristiche di uscita e retta di carico statica. Determinare, da tale grafico, il valore della resistenza di drain R
D.
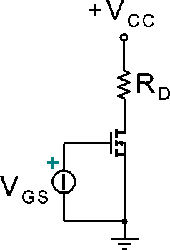
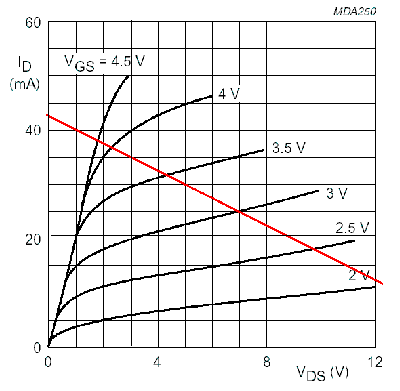
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale
R
D (in Ohm) = 400
Faccio il rapporto Vds / Id (non ho molte alternative) e ottengo (la corrente e' in mA) Rd
Difficoltà: *
Dato il circuito di figura, determinare il valore della resistenza R
C (in kOhm) necessario affinchè il BJT presenti una tensione v
CE a riposo pari a 5 V (si trascuri l'effetto Early).
Dati: R
B=470kOhm, V
CC=12V, V
BE=0.7V, b
F=150
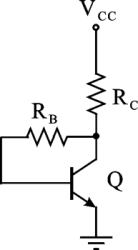
Utilizzare il punto come separatore dei decimali ed inserire i valori numerici con due cifre decimali
R
C (in kOhm) = 5.07
Se Vce=5 V lo e' anche il punto tra Rb e Rc. So anche che Vbe=0.7
Allora ai capi di Rb ho 5-0.7 e posso trovare Ib=(5-0.7)/470k = 0.0091 mA
Trovo allora la corrente che passa su Rc= (b+1) Ib mentre la tensione e' 12-5 V
Rc allora e' uguale a 12-5 / Ib*151 = 5.07 KOhm
Difficoltà: *
Dato il circuito di figura, che rappresenta il modello dinamico equivalente di un amplificatore a transistore bipolare avente un guadagno di corrente b
0 ai piccoli segnali pari a 100, determinare il valore della resistenza di uscita R
OUT indicata in figura. Esprimere tale valore in kOhm.
Dati: R
1=47kOhm, R
2=0.8kOhm, R
3=22kOhm, gm=40mS.
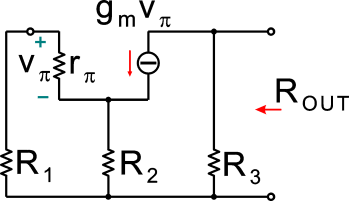
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale
R
OUT (in kOhm) = 22
Siccome non abbiamo corrente che entra per la base, non abbiamo caduta di tensione Vpi, quindi non ho corrente gmVpi, e la Rout = R3.
Difficoltà: **
Dato il circuito di figura, che rappresenta il modello dinamico equivalente di un amplificatore a transistore MOS polarizzato con una corrente di drain a riposo di 0.4 mA (a 25°C), determinare il valore della resistenza equivalente Req indicata in figura (nel calcolo del gm si trascuri l'effetto di modulazione della lunghezza di canale).
Dati: R
1=50kOhm, r
o=10kOhm, V
T=6V,
I
DSS=V
T2mC
oxW/2L=6mA.
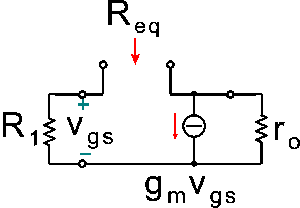
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale
Req (in kOhm) = 318.2
Temibili esercizi con le resistenze equivalenti.
Cominciamo dicendo che R
eq=V
eq/I
eq
Dobbiamo allora cercare Veq in funzione di Ieq, ogni suo termine conterrà Ieq, tutto si semplificherà
e noi risolveremo l'esercizio felici e contenti...
Mettiamo un generatore di tensione Veq ai capi dei morsetti dove calcolare Req, da li uscirà Ieq,
scegliamo un verso, facciamo che la corrente vada verso destra (e li metteremo il capo positivo di Veq). Chiamiamo anche V
Y la tensione che cade sul generatore di corrente, mettiamo il più verso l'alto). Chiamiamo I
O la corrente che passa su R
0 (dall'alto verso il basso)... Scelti i versi, possiamo scrivere le equazioni delle 2 maglie e del nodo in alto...
- Veq-VY-Ieq*R1=0
- Ieq=gm*vgs+IO
- IO*rO-VY=0
Abbiamo 2 incognite I
O e V
Y che devono sparire:
- IO=Ieq-gm*vGS (dalla 2nda)
- (Ieq+gm*Ieq*R1)r0=VY (dalla 3a)
- Veq-(Ieq+gm*Ieq*R1)r0-Ieq*R1=0
Veq=Ieq*R
1+Ieq*r
0+gm*Ieq*R
1*r
0
Req=Veq/Ieq=R
1+r
0+gm*R
1*r
0
e questo è quanto ... = 318198.5 ohm
Difficoltà: **
Dato il circuito di figura, che rappresenta il modello dinamico equivalente di un amplificatore a transistore bipolare polarizzato con una corrente di collettore a riposo di 2mA (a 25°C), determinare il valore della resistenza di ingresso R
IN indicata in figura. Esprimere tale valore in kOhm.
Dati: R
1=100kOhm, R
2=1kOhm, R
3=100kOhm, r
p=2kOhm.
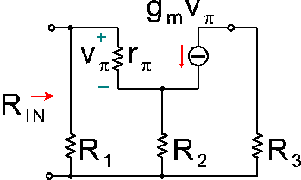
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale
R
IN (in kOhm)= 61.98
Trovo innanzi tutto, sapendo Ic, e sapendo che VT a 25° è 25mV
mi trovo gm=Ic/VT = 0.08
Vedo che la resistenza RIN è pari al parallelo tra R1 e la resistenza che vedo alla destra di R1.
Riduco il problema a calcolare questa resistenza Req. Suppongo che in Rpi passi una corrente Ieq e che ai capi di Req ci sia una tensione Veq.
Allora Req=Veq/Ieq
Veq=Ieq*Rpi + (Ieq+gm*Vpi)*R2
Devo far comparire in ogni termine Ieq (in modo che poi si semplifichi)
Vpi = Ieq*Rpi
sostituendo ottengo
Req=Veq/Ieq = Rpi + (1+gmRpi)R2 =163 Kohm
RIN = Req // R1 = 61.98 Kohm
Difficoltà: **
Dato il circuito di figura, che rappresenta il modello dinamico equivalente di un amplificatore a transistore MOS polarizzato con una corrente di drain a riposo di 2 mA (a 25°C), determinare il valore della resistenza di ingresso RIN indicata in figura (nel calcolo del gm si trascuri l'effetto di modulazione della lunghezza di canale).
Dati: R
1=100kOhm, R
2=1kOhm, R
3=100kOhm, VT=3V, I
DSS=VT2mCoxW/2L=8mA.
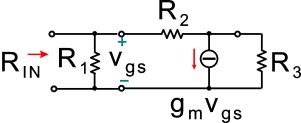
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale
R
IN (in Ohm) =
Difficoltà: **
Dato il circuito di figura, che rappresenta il modello dinamico equivalente di un amplificatore a transistore bipolare avente un guadagno di corrente b
0 ai piccoli segnali pari a 200, determinare il valore della resistenza di uscita R
OUT indicata in figura.
Esprimere tale valore in Ohm.
Dati: R
1=27kOhm, R
2=0.8kOhm, R
3=10kOhm, gm=40mS.
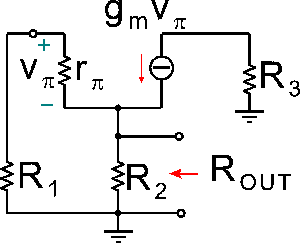
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale
R
OUT (in Ohm)= 132.8
Consideriamo come al solito un generatore Veq applicato ai morsetti di Rout, con la corrente che esce verso l'alto... Abbiamo Ieq = I1 (sulle resistenze R1 e Rpi) + I2 (sulla resistenza R2) + I3 (sulla resistenza R3 verso massa).
I1=Veq / (R1+Rpi)
I2=Veq / R2
I3=-gm*Vpi
Vpi a sua volta è uguale a -I1*Rpi (che possiamo calcolare = 5000 ohm)
Ieq = Veq / (R1+R2) + Veq / R2 + Veq*gmVpi/(R1+Rpi)
per ottenere Req dividiamo per Veq e facciamo il reciproco...
Difficoltà: **
Dato il circuito di figura, che utilizza un amplificatore operazionale ideale, determinare la funzione di trasferimento relativa all'ammettenza d'ingresso Y
IN vista dal generatore V
IN.
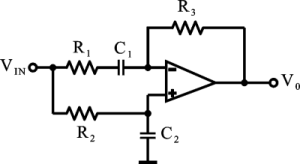
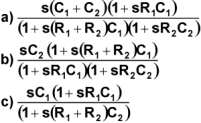
a)
c)
b) (chissà perchè!)
Difficoltà: **
Nel circuito di figura, che usa un amplificatore operazionale ideale, R = 33 kW, C = 10 nF. Determinare il tempo tr (in ms) richiesto affinchè l'uscita si porti ad una tensione di 12 V, se all'ingresso è applicata una tensione vI di -2 V. Si supponga la capacità C inizialmente scarica.
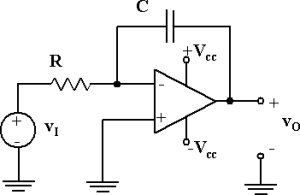
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con due cifre decimali
tr (in ms) = 1.98 ms
Vediamo che la Vo è = alla Vc
Sappiamo (o dovremmo sapere) che per il condensatore Ic=C dV/dt
in questo caso, essendo l'operazionale ideale abbiamo Ic= Vi/R
Da cui Vc = integrale ( - Vi / RC ) dt
poichè tutto è costante mi trovo Vc = Vo = - Vi / RC t
da cui t= Vo/Vi * RC = 1.98 ms
Difficoltà: **
Nel circuito di figura, che usa un amplificatore operazionale ideale, R = 10 kOhm, C = 10 nF. Determinare il valore (in Volt) cui si porta la tensione di uscita dopo 1 ms, se all'ingresso è applicata una tensione v
I di 1 V. Si supponga la capacità C inizialmente scarica.
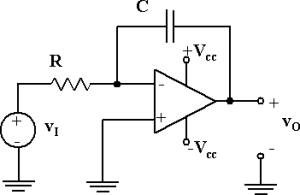
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con due cifre decimali
v
O(1 ms) (in V) = -10
Allo stesso modo dell'esercizio precedente.
Difficoltà: **
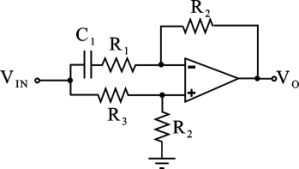
Dato il circuito di figura, che utilizza un amplificatore operazionale ideale, determinare la funzione di trasferimento tra V
IN e V
O.

(NO) b)
c)
a)
Un barbatrucco interessante è questo:
studio il circuito a frequenza zero, ovvero s=jw=0
a frequenza zero il condensatore è un circuito aperto, quindi nel ramo di sopra non passa corrente e mi trovo Vo = V- = V+ = Vin * R2 / (R2+R3)
quindi la funzione di trasferimento è R2 / (R2+R3) se s =0 quindi la possibilità a)
Difficoltà: **
Il circuito di figura rappresenta un transistore MOSFET a canale n polarizzato in zona di saturazione, con relativa transcaratteristica e retta di carico statica. Determinare, da tale grafico, i valori della resistenza di source R
S e della tensione di alimentazione V
DD.
Dati: R
1=200kOhm, R
2=100kOhm
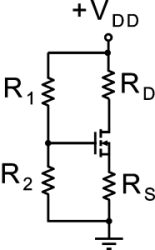
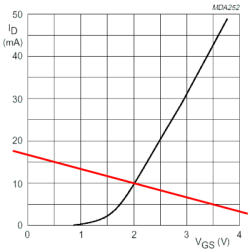
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale
R
S (in Ohm) = 300
V
DD (in V) = 15 V
Difficoltà: **
Dato il circuito di figura, determinare il valore minimo della resistenza RC per il quale il BJT funziona in zona di saturazione (si trascuri l'effetto Early).
Dati: RB=470kOhm, VCC=15V, VBE=-0.7V, VCEsat=-0.5V, bF=150
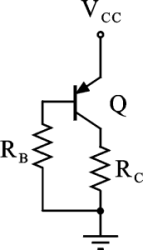
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con due cifre decimali
RCmin(in kOhm)=
Difficoltà: **
Dato il circuito di figura, determinare il valore minimo della resistenza R
C per il quale il BJT funziona in zona di saturazione (si trascuri l'effetto Early).
Dati: R
B=100kOhm, V
CC=25V, V
BE=0.7V, VCEsat=0.8V, b
F=150
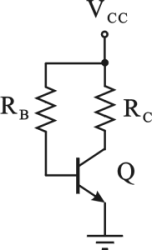
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale
R
Cmin(in Ohm)= 663.9
al limite posso ancora considerare ic= b*Ib
Difficoltà: **
Dato il circuito di figura, determinare l'intervallo di valori della tensione di alimentazione V
DD per il quale il MOSFET funziona in zona di saturazione.
Dati: R
G=80kW, R
D=600W, V
T=4.8V, I
DSS=V
T2mC
oxW/2L=8mA
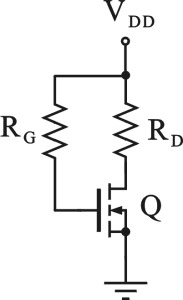 4.8 V < VDD < 9.6V
4.8 V < VDD < 9.6V
(NO) V
DD > 10.2V
V
DD < 6.8V
Su Rg non passa corrente e quindi non cade tensione. Abbiamo allora che Vgs = Vdd
Le condizioni della saturazione, da schemino, sono Vgs>Vt e Vds>Vgs-Vt
Abbiamo allora Vdd>4.8
e Vds>Vdd-Vt
cioe' Vdd<Vds-Vt
Gia' per esclusione visto che deve essere Vdd>4.8 posso scegliere Vdd compreso in [4.8-9.6]
Difficoltà: **
Dato il circuito di figura, determinare il valore della tensione drain-source V
DS a riposo.
Dati: R
1=40kOhm, R
2=40kOhm, R
D=2200Ohm, V
DD=15V, V
T=5V, I
DSS=VT2mCoxW/2L=10mA
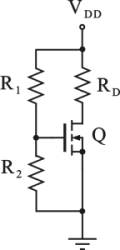
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con due cifre decimali
V
DS (in V) = 9.5
Passo al circuito equivalente dove elimino R1 e R2 e le sostituisco con una Req collegata alla base e ad un generatore equivalente Veq:
Veq (effetto di Vdd) = Vdd*R2/ (R2+R1) = 7.5 V = Vgs
Req = (metto a massa Vdd) = R1//R2 = 20 kOhm
Allora ipotizzo la saturazione (per la quale deve essere Vds > Vgs - Vt = 2.5V)
Id = IDSS + (1-VGS / VT)2 = 2.5 mA
e allora
Vdd = Id * Rd + Vds
da cui Vds = 9.5 V
essendo questo maggiore di 2.5 siamo effettivamente in saturazione e la soluzione e' corretta
Difficoltà: **
Dato il circuito di figura, determinare il valore della resistenza R
C, sapendo che la corrente di collettore a riposo I
C vale 2mA (si trascuri l'effetto Early). Si esprima tale valore in kOhm.
Dati: R
B=270kOhm, V
CC=20V, V
BE=0.7V, b
F=150
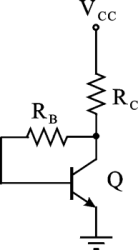
Utilizzare il punto come separatore dei decimali ed inserire i valori numerici con una cifra decimale
R
C (in kOhm)= 7.8
Supponiamo di essere in zona attiva:
ic = 2mA = b * Ib
Vdd = (Ic+Ib)*Rc + Ib*Rb + VBE
da cui RC = (Vdd - Ib*Rb - Vbe) / (Ic+Ib) = 7.79 kOhm
Difficoltà: **
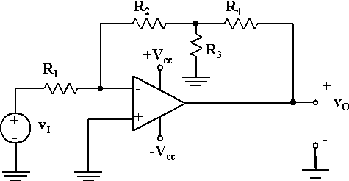
Nell'amplificatore di figura R
1 = R
2 = R
4 = 100 kOhm.
Qual'è il valore di R
3 da utilizzare per ottenere un guadagno il più vicino possibile a -120?
8.47 MOhm
8.47 kOhm
84.7 kOhm
847 OhmLa formula da usare e' Vo = - R2 / R1 (1 + R4/R3 + R4/R2 )
quindi:
-1 (2+ 100k/ R3) = -120
100k/r3=118
R3=100k/118
Difficoltà: **
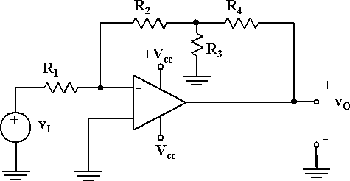
Nell'amplificatore di figura R
1 = R
2 = R
4 = 330 kW. Qual'è il valore di R
3 da utilizzare per ottenere un guadagno il più vicino possibile a -80?
418 W
4.18 kW
41.8 kW
41.8 W
-R2/R1 ( 1 + R2/R3 + R4/R3) = -1 ( 1+1+ 330k /R3) = -80
78=330k/R3
R3=330k/78
Difficoltà: ***
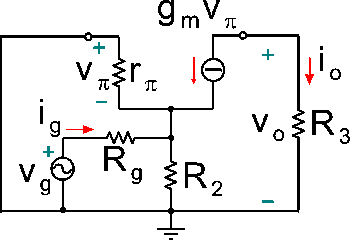
Dato il circuito di figura, che rappresenta il modello dinamico equivalente di un amplificatore a transistore bipolare polarizzato con una corrente di collettore a riposo di 0.4mA (a 25°C), determinare il valore del guadagno di tensione Av=V
o/V
g.
Dati: R
g=2kW, R
2=0.4kW, R
3=2.7kW, r
p=10kW.
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale
Av =
Difficoltà: ***
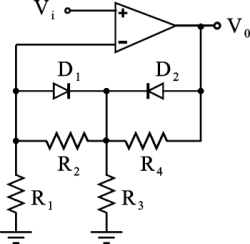
Il circuito di figura, che utilizza un amplificatore operazionale e due diodi ideali, presenta una transcaratteristica Vo = f(Vi) composta da due segmenti, ciascuno di equazione Vo=mVi+q, con un punto di spezzamento in corrispondenza del valore della tensione d'ingresso V
iTH. Determinare:
a) il valore della tensione di spezzamento V
iTH;
b) la pendenza m1 del segmento della transcaratteristica per Vi < V
iTH;
c) il termine noto q1 del segmento della transcaratteristica per Vi < V
iTH;
d) la pendenza m2 del segmento della transcaratteristica per Vi > V
iTH;
e) il termine noto q2 del segmento della transcaratteristica per Vi > V
iTH;
Dati: R
1=5kW, R
2=12kW, R
3=2kW, R
4=10kW.
Utilizzare il punto come separatore dei decimali ed inserire i valori numerici con due cifre decimali
V
iTH (in V) =
m
1 =
q
1 (in V) =
m
2 =
q
2 (in V) =
Difficoltà: ***
Il circuito di figura, che utilizza un amplificatore operazionale ideale e due diodi aventi una tensione di soglia V
g=0.5V, presenta una transcaratteristica Vo = f(V
i) che, considerando solo valori negativi della tensione d'ingresso, è composta da due segmenti, ciascuno di equazione Vo=mVi+q, con un punto di spezzamento in corrispondenza del valore della tensione d'ingresso V
iTH. Determinare:
a) il valore della tensione di spezzamento V
iTH;
b) la pendenza m
1 del segmento della transcaratteristica per Vi < V
iTH;
c) il termine noto q
1 del segmento della transcaratteristica per Vi < V
iTH;
d) la pendenza m
2 del segmento della transcaratteristica per V
iTH < Vi < 0
e) il termine noto q
2 del segmento della transcaratteristica per V
iTH < Vi < 0
Dati: R
1=10kW, R
2=4kW, R
3=2kW, R
4=20kW.
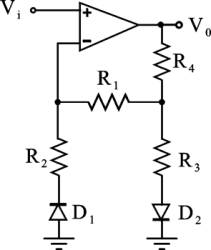
Utilizzare il punto come separatore dei decimali ed inserire i valori numerici con due cifre decimali
V
iTH (in V) = -0.5
m
1 = 8.5
q
1 (in V) = 3.75
m
2 = 1
q
2 (in V) = 0
Difficoltà: ***
Il circuito di figura, che utilizza un amplificatore operazionale ed un diodo entrambi considerati ideali, presenta una transcaratteristica Vo = f(Vi) composta da due segmenti, ciascuno di equazione Vo=mVi+q, con un punto di spezzamento in corrispondenza del valore della tensione d'ingresso V
iTH. Determinare:
a) il valore della tensione di spezzamento V
iTH;
b) la pendenza m1 del segmento della transcaratteristica per Vi < V
iTH;
c) il termine noto q1 del segmento della transcaratteristica per Vi < V
iTH;
d) la pendenza m2 del segmento della transcaratteristica per Vi > V
iTH;
e) il termine noto q2 del segmento della transcaratteristica per Vi > V
iTH;
Dati: R
1=1kW, R
2=8kW, R
3=3kW, R
4=1kW, R
5=4kW.
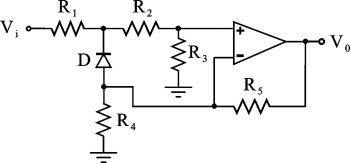
Utilizzare il punto come separatore dei decimali ed inserire i valori numerici con due cifre decimali
V
iTH (in V) = 0
m1 = -4
q
1 (in V) = 0
m
2 = -1.24
q
2 (in V) = 0
Difficoltà: ***
Dato il circuito di figura, determinare i valori delle quattro resistenze che garantiscono il funzionamento del MOSFET nelle seguenti condizioni: I
D=4 mA, V
D=V
DD/2, V
DS=V
DD/4 e che la massima potenza dissipata dal circuito sia 75 mW.
Dati: V
DD=18V, V
T=4V, I
DSS=VT2mC
oxW/2L=10mA

.
Utilizzare il punto come separatore dei decimali ed inserire i valori numerici con due cifre decimali
R
D(in kW) = 2.25
R
S(in kW) = 1.13
R
1(in kW) = 66.18
R
2(in kW) = 41.82
Ai capi di Rd abbiamo VDD e VD e la corrente ID, trovo quindi RD = 9 / ID = 1125 ohm.
So tutto anche per trovare RS = 4.5 / ID = 2250 ohm.
So anche che nel ramo di sinistra, passa per R1+R2 una corrente I1=Vdd/R1+R2
Posso scrivere l'equazione della potenza:
P = I12(R1+R2)+ID2(Rd+Rs)+VDS*ID
conosco tutto tranne la I1, me la ricavo, e trovo che R1+R2=108000 ohm
A questo punto mi trovo dall'equazione (per i MOS in saturazione) della ID, il valore della VGS... che risulta = 6.53 V.
Ora so che il nodo tra R1 e R2, sarà a potenziale Vgs+Vs (la tensione del morsetto source=4.5 V), mi ricavo, conoscendo I1 il valore di R1=66178.7 ohm e, sottraendo da 108000, anche il valore di R2=41821,2 ohm.
Difficoltà: ***
Dato il circuito di figura, determinare il punto di lavoro I
C, V
CE del BJT (si trascuri l'effetto Early).
Dati: R
B=270kOhm, R
C=1.8kOhm, V
CC=15V, V
BE=0.7V, b
F=150
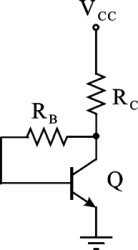
Utilizzare il punto come separatore dei decimali ed inserire i valori numerici con una cifra decimale
I
C (in mA)= 4
V
CE (in V)= 7.8
Le 2 equazioni delle maglie sono
Vcc = Rc (b+1) Ib + Ib Rb + Vbe
da cui ricavo Ib=0.03 mA e Ic=b * Ib = 4 mA
e
Vcc = (b+1) Ib Rc + Vce
Da cui ricavo Vce = 7.8 V



 Utilizzare il punto come separatore ed inserire il valore numerico con due cifre decimali.
Utilizzare il punto come separatore ed inserire il valore numerico con due cifre decimali. Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con due cifre decimali
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con due cifre decimali 4.2V < VDD < 7.4V
4.2V < VDD < 7.4V Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con due cifre decimali
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con due cifre decimali PIB = 100 mW
PIB = 100 mW (NO) b) ZIN(¥) = 2R
(NO) b) ZIN(¥) = 2R Rin = R3
Rin = R3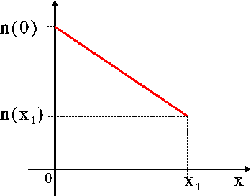
 Inserire il valore utilizzando il punto come separatore dei decimali ed utilizzando una cifra decimale
Inserire il valore utilizzando il punto come separatore dei decimali ed utilizzando una cifra decimale
 Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale Utilizzare il punto come separatore dei decimali ed inserire i valori numerici con due cifre decimali
Utilizzare il punto come separatore dei decimali ed inserire i valori numerici con due cifre decimali Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale
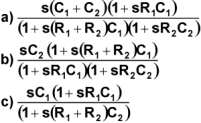 a)
a) Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con due cifre decimali
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con due cifre decimali Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con due cifre decimali
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con due cifre decimali
 (NO) b)
(NO) b)
 Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con due cifre decimali
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con due cifre decimali Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale
 Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con due cifre decimali
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con due cifre decimali Utilizzare il punto come separatore dei decimali ed inserire i valori numerici con una cifra decimale
Utilizzare il punto come separatore dei decimali ed inserire i valori numerici con una cifra decimale 8.47 MOhm
8.47 MOhm 418 W
418 W Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale
Utilizzare il punto come separatore dei decimali ed inserire il valore numerico con una cifra decimale Utilizzare il punto come separatore dei decimali ed inserire i valori numerici con due cifre decimali
Utilizzare il punto come separatore dei decimali ed inserire i valori numerici con due cifre decimali Utilizzare il punto come separatore dei decimali ed inserire i valori numerici con due cifre decimali
Utilizzare il punto come separatore dei decimali ed inserire i valori numerici con due cifre decimali Utilizzare il punto come separatore dei decimali ed inserire i valori numerici con due cifre decimali
Utilizzare il punto come separatore dei decimali ed inserire i valori numerici con due cifre decimali .
Utilizzare il punto come separatore dei decimali ed inserire i valori numerici con due cifre decimali
.
Utilizzare il punto come separatore dei decimali ed inserire i valori numerici con due cifre decimali Utilizzare il punto come separatore dei decimali ed inserire i valori numerici con una cifra decimale
Utilizzare il punto come separatore dei decimali ed inserire i valori numerici con una cifra decimale